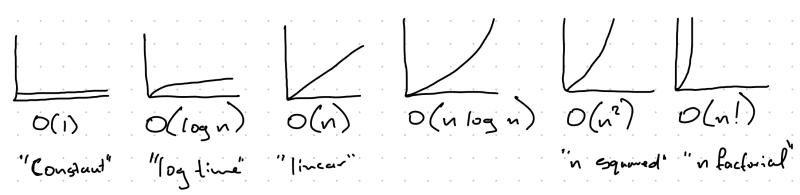This is a fun one! Communicating with Big O is one of the first face-melting transitions for early career devs.
Let's look at why.
But first, a pit stop. Do you remember those absolutely rediculous word problems from grade school?
Sally went to the grocery store and bought 37 watermelons. She had $20 dollars. Each watermelon costs $0.70. How much money does Sally have when she gets home?
Were you left wondering, "How in the world is Sally going to get home? With 37 watermelons?! $6.00 isn't going to be enough to get an Uber with enough space for the melons... what is Sally doing?!"
Silly Sally.
Some folks say this is losing the forest for the trees. I say it's just a terribly lazy way to construct practice problems.
The purpose of Big O Notation is to be able to talk, literally communicate with other people, about a quality of our craft. The particular focus here is to enable the comparison between solutions in the worst-case scenario as the size of the input increases.
We want to be able to talk about potential solutions (the same thing as saying: algorithms) in the abstract. This is a crucial point: in the abstract. We don't care, at all, about the data we have. When we play with these ideas we assume a theoretically gigantic, but finite dataset.
When we think about the data we have, this is reasoning in the concrete. When we think of Big O Notation, we're reasoning in the abstract. Its EASY to fall back to concrete reasoning. This is where we spend most of life. It's easy, usually obvious, and comfortable.
Should I cross the street now? Is there a car? No? Okay, cross.
Don't do it when reasoning in the abstract!
Definitions, quickly
Do you mind if I do you a favor here? There's a bunch of math terms that might also get in the way. Here's a visual, in order, from best case to worst, for the some common Big O terms. We need these so we can do the thinking & learning instead of getting stuck on terminology.
O(1) - "Constant Time"
It doesn't matter how big the input is, the system always returns the result in the same amount of time.
O(log n) - "Log Time"
As the solution (or algorithm) iterates over the input, each iteration gets faster!
O(n) - "Linear Time"
As the algorithm iterates, each iteration takes the same amount of time as the previous iteration.
O(n log n) - no fancy terminology here
Shows that the ideas can be combined (yikes). As we iterate, each iteration gets slower, but gets slower fairly slowly.
O(n^2) - "n squared"
For each iteration, the iterations get slower pretty quickly.
O(n!) - "n factorial"
For each iteration, the iterations get slower super fast.
The goal is to try to stay as far away as possible from "n factorial" and try not to get much worse than Constant.
With all that understood, let's now try to bridge the gap.
Bridging the Gap Between Concrete and Abstract Thinking
Understanding Big O Notation
Big O notation is used to describe the performance or complexity of an algorithm (solution). It provides a high-level understanding of how an algorithm (solution) will perform as the size of the input grows. For example, an algorithm with O(n) complexity will have its run time increase linearly with the size of the input.
Concrete vs Abstract Thinking
The challenge arises when developers mistake reasoning about specific data for reasoning about the algorithm itself. Phrases like, "but this data is real," may signal this confusion. While reasoning about the real data can help you get started, it's vital to separate the solution from the current input.
Why the Misunderstanding?
Early career developers might make this mistake due to lack of experience with larger-scale problems or being too engrossed in the specifics of a current problem. It's essential to separate the concrete details from the abstract complexity to create scalable solutions.
Practical Consequences
When the input increases by 100 or 100,000 fold, what happens to the algorithm? An incredibly complex solution complexity might fall apart with a larger dataset. An algorithm that seems fine for small data sets might fail dramatically with larger ones, leading to performance issues and other challenges.
Learning to Think in the Abstract
Developing the ability to think abstractly about problems requires practice and guidance. Some strategies include:
- Creating abstract models: Representing problems in a generalized way.
- Analyzing algorithms separately from data: Evaluating how the algorithm behaves irrespective of specific data points.
- Building scaling scenarios: Imagining how the algorithm will perform with varying sizes of input.
Abstract thinking in general, and Big O Notation specifically, are essential skills in algorithm (solution!) design. By learning to separate problem complexity from algorithm complexity, developers can avoid common pitfalls and enhance their problem-solving abilities when working alone AND dramatically enhance the ability to work together with other folks who have similarly invested the time to learn how to communicate this way.
Complex problems don’t often require complex solutions. (Sally probably didn’t need 37 watermelons to begin with... what's she gonna do with 37 watermelons?!)