Introduction:
Dynamic Programming (DP) is a powerful problem-solving technique that is widely used in computer science and programming. It provides an efficient way to solve problems by breaking them down into smaller subproblems and storing their solutions to avoid redundant computations. In this blog, we'll delve into the world of Dynamic Programming, exploring its core concepts and showcasing its application through real-world problems.

Understanding Dynamic Programming:

Dynamic Programming involves solving a problem by breaking it into smaller overlapping subproblems and storing the solutions to those subproblems for future use. The key idea is to avoid redundant calculations and save time by reusing previously computed results.

Fibonacci Sequence:

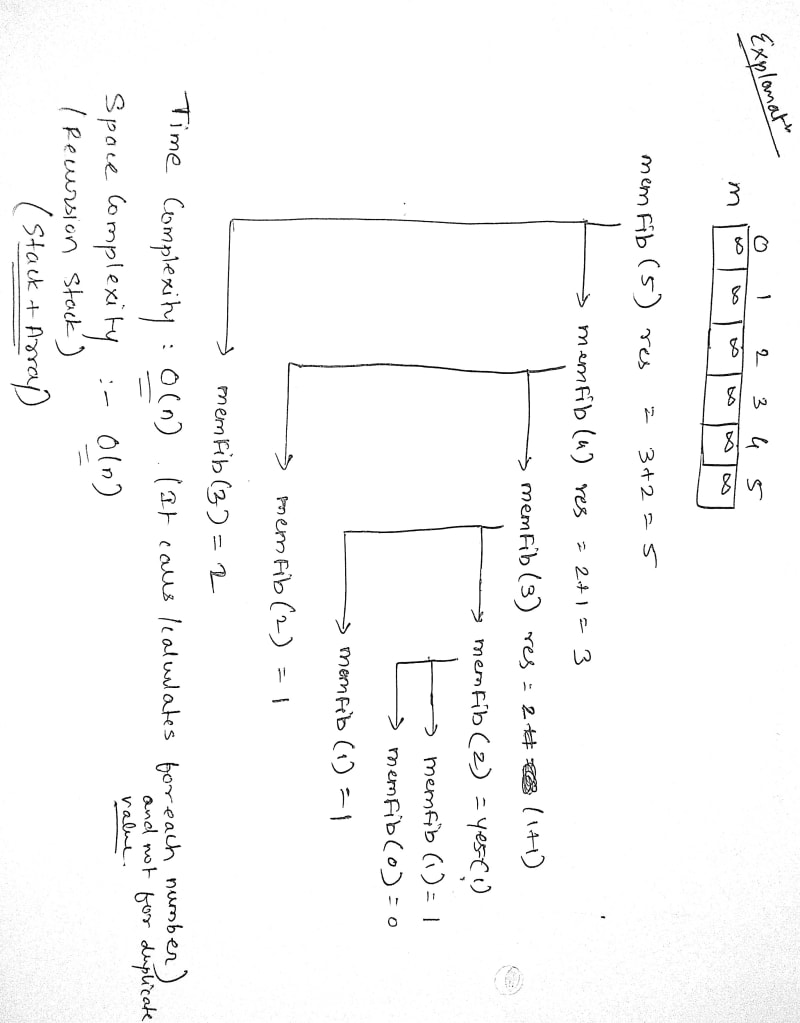
One of the classic examples of Dynamic Programming is calculating the nth Fibonacci number. Without DP, this problem has an exponential time complexity due to redundant calculations. By using memoization (storing computed results) or tabulation (building up solutions iteratively), DP reduces the complexity to linear time.

The Fibonacci sequence starts with 0 and 1. Each subsequent number is the sum of the two preceding numbers. Mathematically, it can be represented as:

F(0) = 0
F(1) = 1
F(n) = F(n-1) + F(n-2) for n > 1

1.Memoization:

Memoization involves storing calculated results in a data structure (like an array or a hash map) so they can be easily retrieved when needed. When a Fibonacci number is computed, it's stored for future reference. Subsequent calculations simply retrieve the stored results. This drastically reduces the number of redundant calculations.

2.Tabulation:

Tabulation takes a bottom-up approach. It starts with the base cases (F(0) and F(1)) and iteratively computes Fibonacci numbers up to the desired value. The results are stored in an array. This approach is efficient as it doesn't rely on function calls and recursion.

Dynamic Programming in Action: Fibonacci Sequence

Let's take the example of calculating F(5) using both memoization and tabulation:

1.Memoization:

Calculate F(0) and F(1) and store them.
Calculate F(2) by retrieving F(1) and F(0), and store it.
Calculate F(3) by retrieving F(2) and F(1), and store it.
Calculate F(4) by retrieving F(3) and F(2), and store it.
Calculate F(5) by retrieving F(4) and F(3), and store it.

Certainly, here's a C code example for calculating the Fibonacci series using dynamic programming (DP) with the memoization technique. This code is tailored for a Dev.to post:

#include <stdio.h>

// Maximum number of terms in the Fibonacci series
#define MAX 100

// Initialize the memoization table
long long memo[MAX];

// Initialize memoization table with default values
void initializeMemo() {
    for (int i = 0; i < MAX; i++) {
        memo[i] = -1;
    }
}

// Calculate Fibonacci number using memoization
long long fib(int n) {
    if (memo[n] != -1) {
        return memo[n];
    }

    if (n <= 1) {
        return memo[n] = n;
    }

    return memo[n] = fib(n - 1) + fib(n - 2);
}

This code defines a fib function that calculates the nth Fibonacci number using memoization. The initializeMemo function initializes the memoization table with default values. The main function takes input for the number of terms in the Fibonacci series and prints the Fibonacci series up to the given number of terms using the fib function.

Feel free to use this code snippet in your Dev.to post, and make sure to provide a clear explanation of how memoization works and how it improves the efficiency of calculating Fibonacci numbers.

2.Tabulation:

Initialize an array to store Fibonacci numbers.
Calculate F(0) and F(1) and store them in the array.
Iterate from 2 to 5, calculating F(i) using F(i-1) and F(i-2), and storing the results in the array.

#define MAX 100
long long dp[MAX];

void initializeDP() {
    dp[0] = 0;
    dp[1] = 1;
}

void fibTabulation(int n) {
    for (int i = 2; i <= n; i++) {
        dp[i] = dp[i - 1] + dp[i - 2];
    }
}

Conclusion

Using dynamic programming with memoization, the Fibonacci series can be computed efficiently with reduced time complexity. This approach avoids redundant calculations, making it ideal for generating larger Fibonacci sequences. The use of memoization significantly enhances the performance and showcases the power of dynamic programming in solving classic problems.